Cinemática
Dinámica
El trabajo y la energía
El trabajo
El trabajo se define como la cantidad escalar dada por: \begin{equation} W=\int \vec{F}\cdot \mathrm{d}\vec{r} \end{equation} Recuérdese que el producto punto es la proyección de un vector sobre otro. Por lo tanto, el trabajo es igual a la integral de la proyección de la fuerza aplicada \(\vec{F}\) a lo largo de la trayectoria \(\vec{r}\) descrita por el cuerpo sobre el que actúa la fuerza.
El trabajo tiene unidades de fuerza por distancia: \[ \left[W\right]=\left[\vec{F}\cdot \mathrm{d}\vec{r}\right]=\mathrm{N}\cdot \mathrm{m}=\mathrm{Joule} \] El Joule es la unidad de "energía" del sistema internacional, pero ¿qué es la energía?
Regresa al inicioLa energía
La energía es un concepto abstracto que surge de la observación de que existe una cantidad física que en un sistema cerrado se conserva.
La energía es una medida de las acciones que se ejercen sobre un sistema dado y esta cantidad obedece una ley universal de conservación. La energía no se crea ni se destruye, únicamente se transforma de una forma a otra.
Regresa al inicioTeorema del trabajo y la energía
El trabajo expresa la habilidad de una fuerza de ejercer un cambio en la energía de un cuerpo o sistema. Considere una partícula de masa \(m\) que se mueve bajo la influencia de una fuerza neta constante, \( \vec{F}=\mathrm{cte} \) ( i.e. \( \vec{a}=\mathrm{cte.} \) ).
Si la partícula se desplaza una distancia \( d=(x_f-x_i) \) en la dirección de la fuerza, \begin{align*} \Rightarrow W&=\int\limits_{x_i}^{x_f} \vec{F}\cdot \mathrm{d}\vec{x} =F \int\limits_{x_i}^{x_f} \mathrm{d}x = F x \Big|_{x_i}^{x_f}= F(x_f-x_i)\\ &=F\times d=(m a) d \end{align*} donde \( F \) y \(a\) son respectivamente las magnitudes de la fuerza y de la aceleración. Ahora recordando nuestros conceptos de cinemática podemos escribir \[ d=\frac{1}{2}(v_i+v_f) t \] \[ a=\frac{(v_f-v_i)}{t} \] con \(v_i=v(t=0)\) y \(v_f=v(t)\) como las velocidades instantáneas al momento cuando se inicia el desplazamiento \(d\) y al tiempo \(t\) cuando se ha realizado el desplazamiento. Sustituyendo en la fórmula del trabajo \[ W=m\left(\frac{v_f-v_i}{t}\right) \frac{1}{2}\left(v_f-v_i\right) t \\ =\frac{1}{2}m\left(v_f-v_i\right) \left(v_f+v_i\right) \] \[ \Rightarrow W=\frac{1}{2}m v_f^2-\frac{1}{2}m v_i^2 \] Observe que en efecto cada uno de los dos términos de la expresión anterior tienen unidades de trabajo: \[ \left[ \frac{1}{2}m v^2 \right]= \mathrm{kg} \left(\mathrm{m/s}\right)^2= \left(\mathrm{kg\, m/s^2}\right)\, m=\mathrm{N\, m}=\mathrm{Joule} \]
Además, cada uno de los dos términos de la expresión dependen únicamente del estado de movimiento de la partícula en el momento inicial y final del desplazamiento. Por lo tanto, cada uno de estos términos pueden identificarse como la energía asociada el estado de movimiento de la partícula antes y después de aplicada la fuerza, por lo que el trabajo realizado puede ser identificado como el cambio de la energía de la partícula. Esto es, podemos definir a la energía cinética de una partícua de masa \(m\) que se mueve a una velocidad \(v\) de la siguiente manera: \begin{equation} K=\frac{1}{2}m v^2 \end{equation} De esta forma, el teorema de trabajo-energía resulta de relacionar al trabajo realizado por la fuerza con el cambio en la energía cinética: \[ W=K_f-K_i=\Delta K \]
Este mismo procedimiento lo podemos repetir aún si la fuerza no es constante: \[ W=\int\limits_{x_i}^{x_f}F_x\cdot \mathrm{d}x=\int\limits_{x_i}^{x_f}m a_x\cdot \mathrm{d}x \] Utilizando la regla de la cadena \( a_x=\frac{\mathrm{d}v}{\mathrm{d}t}=\frac{\mathrm{d}v}{\mathrm{d}x}\frac{\mathrm{d}x}{\mathrm{d}t}=v\frac{\mathrm{d}v}{\mathrm{d}x} \) \[ \Rightarrow \hspace{1cm} W=\int\limits_{x_i}^{x_f}m v\frac{\mathrm{d}v}{\mathrm{d}x}\cdot \mathrm{d}x=\int\limits_{v_i}^{v_f}m v \,\mathrm{d}v \] \[ \therefore \hspace{1cm} W=\frac{1}{2}m v_f^2-\frac{1}{2}m v_i^2 \]
Regresa al inicioLa energía potencial
La energía potencial es energía almacenada en un sistema que puede realizar trabajo o transformarse en energía cinética. La energía potencial la podemos asociar a fuerzas conservativas para las que la energía cinética ganada ó perdida por un sistema conforme sus constituyentes cambian sus posiciones relativas es balanceada por una pérdida o ganancia igual en energía potencial. Esto da lugar al principio de conservación de la energía mecánica.
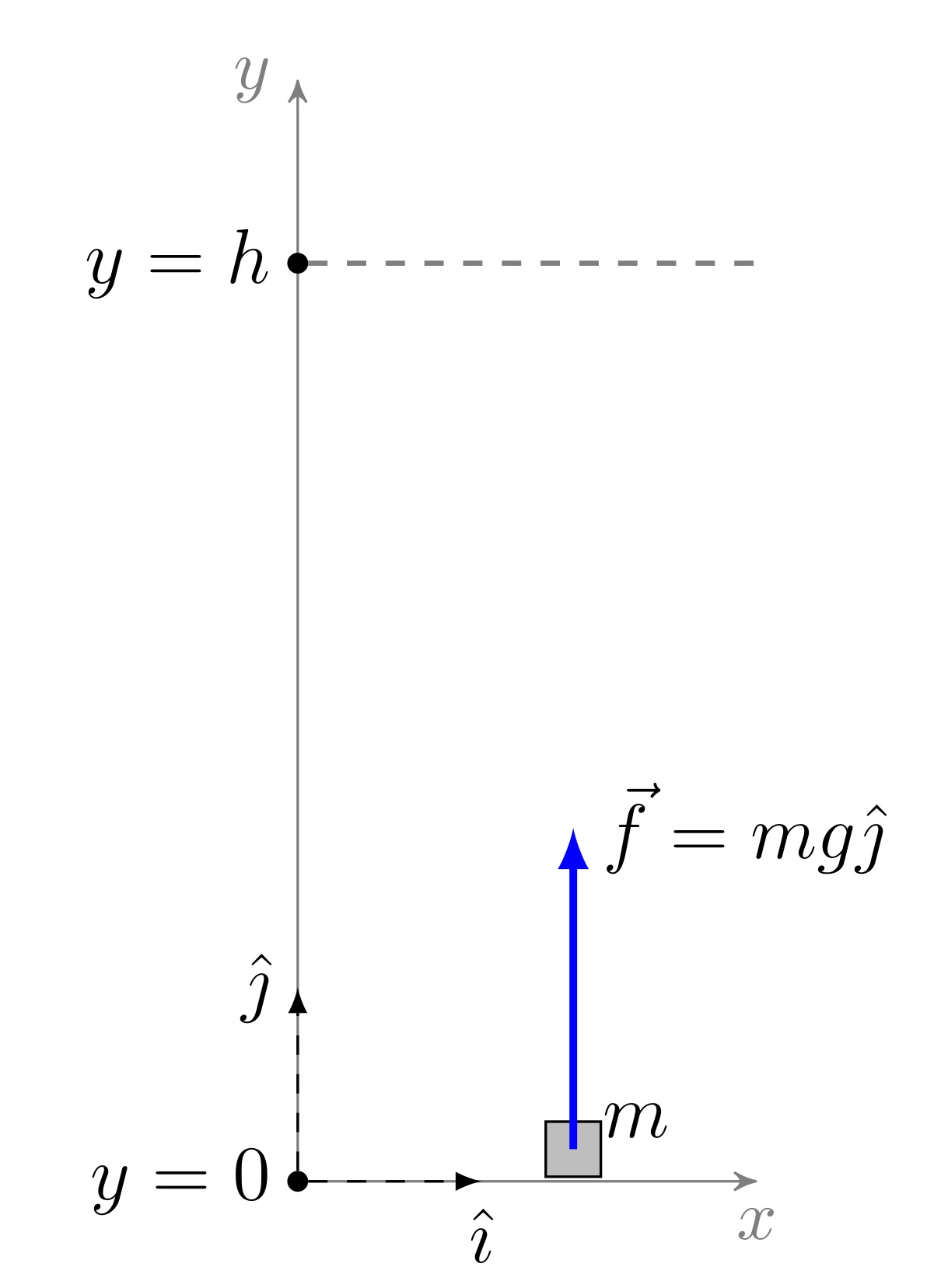
Hagamos un ejercicio simple. ¿Cuál es la energía potencial de un cuerpo de masa \(m \) que se encuentra a una altura \(h\) con respecto al piso? Para resolver este problema calculemos la cantidad de trabajo que realizaría el campo de fuerza gravitacional sobre el cuerpo cuando este se deja caer desde la altura \(h\) y llega hasta el suelo. \[ W=\int\limits_{h}^{0}\vec{F}\cdot \mathrm{d}y=(-mg) y\Big|_{h}^{0}=(-mg)(0-h)=mgh \] Si ahora definimos a $U_g$ como la energía potencial gravitacional de modo que \(U_g=0\) en el suelo (\(y=0\), entonces necesariamente a una altura \(y=h\) tendremos que \[ U_g(y=h)=mgh \] Por lo tanto, el cambio en la energía potencial sufrido por el cuerpo en su desplazamiento entre la altura \(h\) y el suelo está dado por: \[ \Delta U_g=U_g(y=0)-U_g(y=h)=0-mgh=-mgh \]
Podemos ahora extender este mismo concepto para dos alturas arbitrarias y calcular el trabajo requerido para mover al objeto desde una posición inicial hasta una final: \[ W_g=-(U_f-U_i)=-\Delta U_g \] Esto quiere decir que el trabajo realizado sobre un cuerpo por la fuerza gravitacional es igual al negativo del cambio en la energía potencial gravitacional del sistema.
En general, el trabajo realizado por una fuerza conservativa es igual al negativo cambio de la energía potencial generada por la fuerza en el espacio. \begin{equation} W=-\Delta U \end{equation}
Problemas de trabajo y energía
- ¿Cuánto trabajo se realiza en contra de la gravedad al levantar un objeto de \(3\) kg a lo largo de una distancia vertical de \(40\) cm?
-
¿Cuánto trabajo realiza sobre un objeto una fuerza que lo sostiene mientras el objeto es descendido a través de una distancia vertical \(h\)? ¿Cuánto trabajo realiza la fuerza de gravitación en este objeto al realizar el mismo proceso?
Solución: El trabajo realizado por quien sostiene el objeto mientras desciende: \[ W_{f}=\int\limits_{h}^{0}\vec{F}\cdot \mathrm{d}y = F \int\limits_{h}^{0} \mathrm{d}y= (mg) y \Big|_{h}^{0}=(mg)(0-h) = -mgh \] Por otro lado, como se vió anteriormente, el trabajo realizado por la fuerza de gravedad es: \[ W_G=\int\limits_{h}^{0}\vec{F}\cdot \mathrm{d}y = F \int\limits_{h}^{0} \mathrm{d}y = (-mg) y\Big|_{h}^{0} = (-mg)(0-h) = mgh \]
- Calcule el trabajo realizado en contra de la gravedad por una bomba que descarga \(600\) litros de combustible en un tanque que se encuentra \(20\) m por encima de la toma de la bomba. \( 1\) cm\(^3\) de combustible tiene una masa de \(0.82\) g. \(1\) lt es igual a \(1000\) cm\(^3\).
- Una masa de \(2\) kg cae \(400\) cm. (a) ¿Cuánto trabajo ha realizado sobre esta masa la fuerza gravitacional? (b) ¿Cuánta energía potencial gravitacional ha perdido esta masa?
- Un bloque de \(0.5\) kg se desliza sobre la superficie de una mesa con una velocidad inicial de \(20\) cm/s y alcanza el reposo en una distancia de \(70\) cm. Encuentre la fuerza de fricción promedio que frenó este movimiento.
Solución: Este problema se puede resolver utilizando únicamente argumentos de trabajo y energía. Para empezar, el trabajo realizado por la fuerza de fricción es: \[ W= \int\limits_{x_i}^{x_f} \vec{F} \cdot \mathrm{d}\vec{x} = F \int\limits_{x_i}^{x_f} \mathrm{d}x =F(x_f-x_i)= F\, d \] Esto debido a que la magnitud \(F\) de la fuerza de fricción cinética es constante y su dirección es siempre paralela pero con sentido contrario al desplazamiento. A la vez, el teorema de trabajo y energía indica que este trabajo debe de ser igual al cambio en la energía cinética: \[ W = \Delta K = \frac{1}{2} m v_f^2-\frac{1}{2} m v_i^2 = - \frac{1}{2} m v_i^2 \] Por lo tanto, la fuerza de fricción es: \[ F = - \frac{m v_i^2}{2 d} \] Si resolvemos esto utilizando el procedimiento desarrollado en la sección de cinemática tendríamos posiblemente que: \[ a = \frac{v_f^2-v_i^2}{2 d} = -\frac{v_i^2}{2 d} \] Luego, por la 2a ley de Newton tenemos que \[ F= m a = -\frac{m v_i^2}{2 d} \] que es el mismo resultado al que llegamos antes.
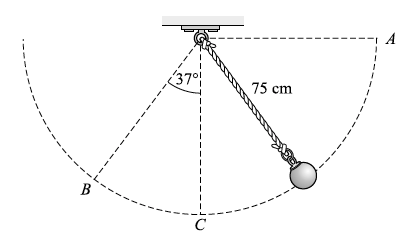
- Considere el péndulo simple mostrado en la figura. (a) Si la bola es liberada desde el punto A, ¿cuál será la velocidad de la bola cuando esta pase a través del punto C? (b) ¿Cuál es la velocidad de la bola en el punto B?
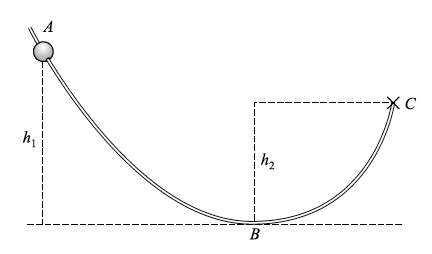
- La figura muestra una cuenta resbalando en un alambre. ¿Qué tan grande debe de ser la altura \( h_1 \) para que la cuenta, iniciando desde el reposo en el punto A, alcance una velocidad de \( 200\) cm/s en el punto B?
- Suponga que \(h_1=50\) cm, \(h_2= 30\) cm, la longitud a lo largo del alambre desde A hasta C es de \(400\) cm, y una cuenta de \(3\) g liberada desde A alcanza el punto C donde se detiene. ¿Qué tan grande es la fuerza de fricción promedio que se opone a este movimiento?
El péndulo simple (energía)
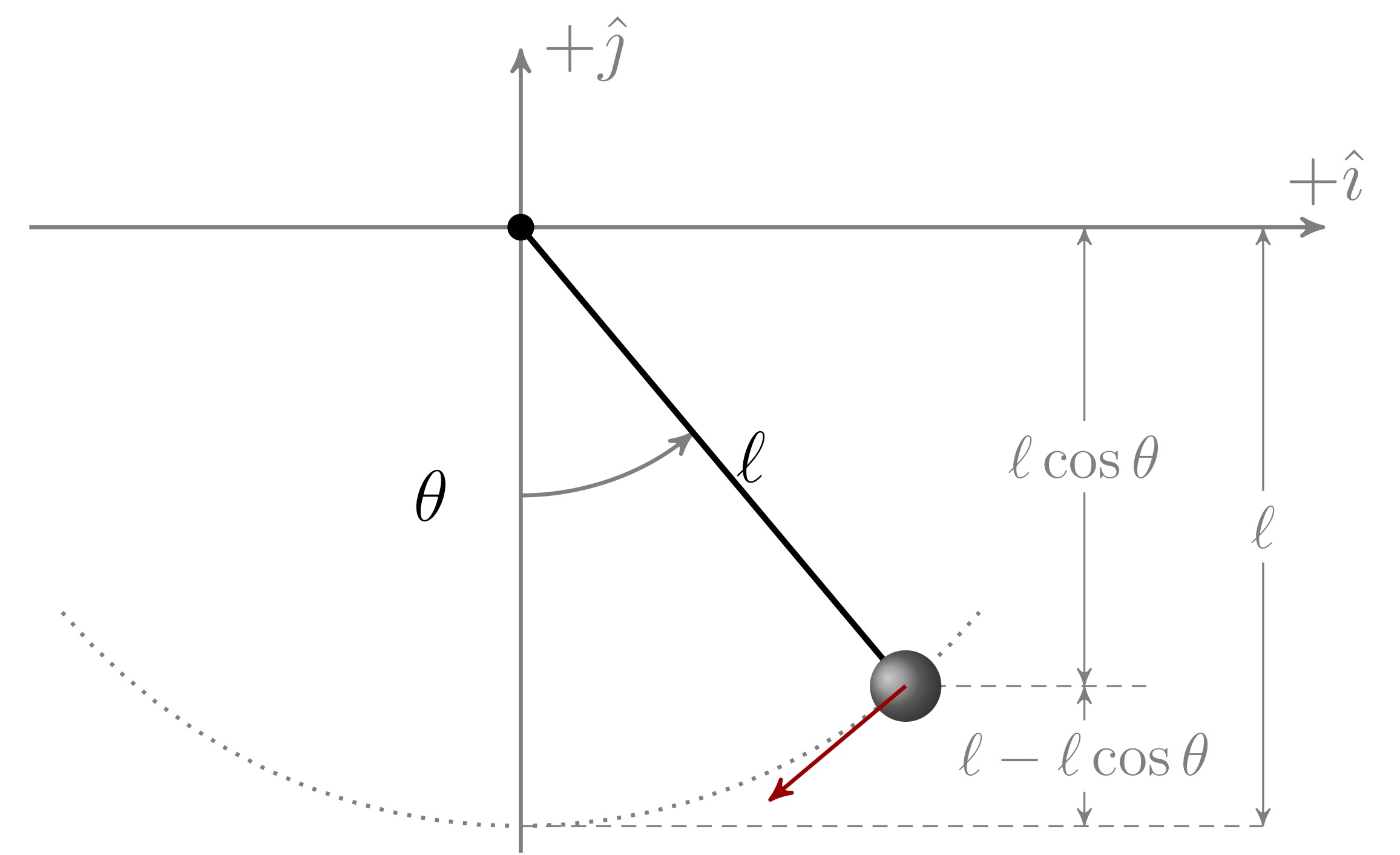
Energía potencial: \[ U_g=mg\ell \left(1-\cos \theta \right) \] Energía cinética: \[ K=\frac{1}{2} m v^2= \frac{1}{2} m (\ell \dot{\theta})^2 \] con \(v=\ell \frac{\mathrm{d}}{\mathrm{d}t}\theta=\ell \dot{\theta} \).
La energía total del péndulo es: \begin{align*} U_g+K &= E \\ mg\ell \left(1-\cos \theta \right) + \frac{1}{2} m (\ell \dot{\theta})^2 &=E \end{align*} La energía se conserva, así que \(E\) es una constante y su derivada debe de ser igual a cero: \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} E &= 0 \\ \frac{\mathrm{d}}{\mathrm{d}t} \left[ mg\ell \left(1-\cos \theta \right) \right]+ \frac{\mathrm{d}}{\mathrm{d}t} \left[ \frac{1}{2} m (\ell \dot{\theta})^2 \right] &=0 \\ -mg \ell \frac{\mathrm{d}}{\mathrm{d}t} \cos \theta + \frac{1}{2} m \ell^2 \frac{\mathrm{d}}{\mathrm{d}t} \dot{\theta}^2 &=0 \\ mg\ell \sin \theta \dot{\theta} + m \ell^2 \dot{\theta} \ddot{\theta} &= 0 \\ g \sin \theta + \ell \ddot{\theta} &= 0 \end{align*} Por consiguiente la ecuación de movimiento que se obtiene es: \[ \ddot{\theta} = -\frac{g}{\ell} \sin \theta \] En el límite de oscilaciones pequeñas \[ \lim_{\theta\to 0}(\sin \theta)=\theta \] se tiene la ecuación diferencial del oscilador armónico simple \[ \ddot{\theta} = -\frac{g}{\ell} \theta \]
Regresa al inicioMensajes
Otros
- Videos del profesor Walter Lewin en el MIT:
- Harvard Natural Sciences Lecture Demonstrations: